URLCrazy

Download urlcrazy-0.5.tar.gz
Latest Version 0.5, July 2012
License Restrictive. See README file.
Author Andrew Horton (urbanadventurer)
Kali Linux https://tools.kali.org/information-gathering/urlcrazy

Introduction

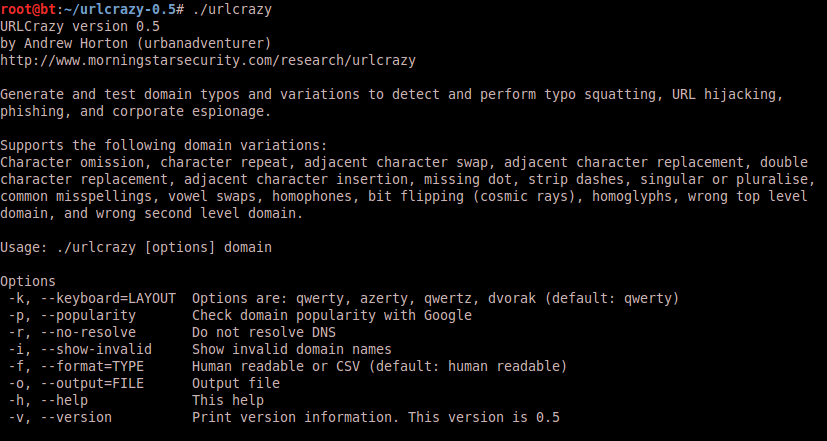
URLCrazy allows you to generate and test domain typos and variations to detect and perform typo squatting, URL hijacking, phishing, and corporate espionage.

Usage

• Detect typo squatters profiting from typos on your domain name
• Protect your brand by registering popular typos
• Identify typo domain names that will receive traffic intended for another domain
• Conduct phishing attacks during a penetration test

Features

• Generates 15 types of domain variants
• Knows over 8000 common misspellings
• Supports cosmic ray induced bit flipping
• Multiple keyboard layouts (qwerty, azerty, qwertz, dvorak)
• Checks if a domain variant is valid
• Test if domain variants are in use
• Estimate popularity of a domain variant URLCrazy requires Linux and the Ruby interpreter.

Usage

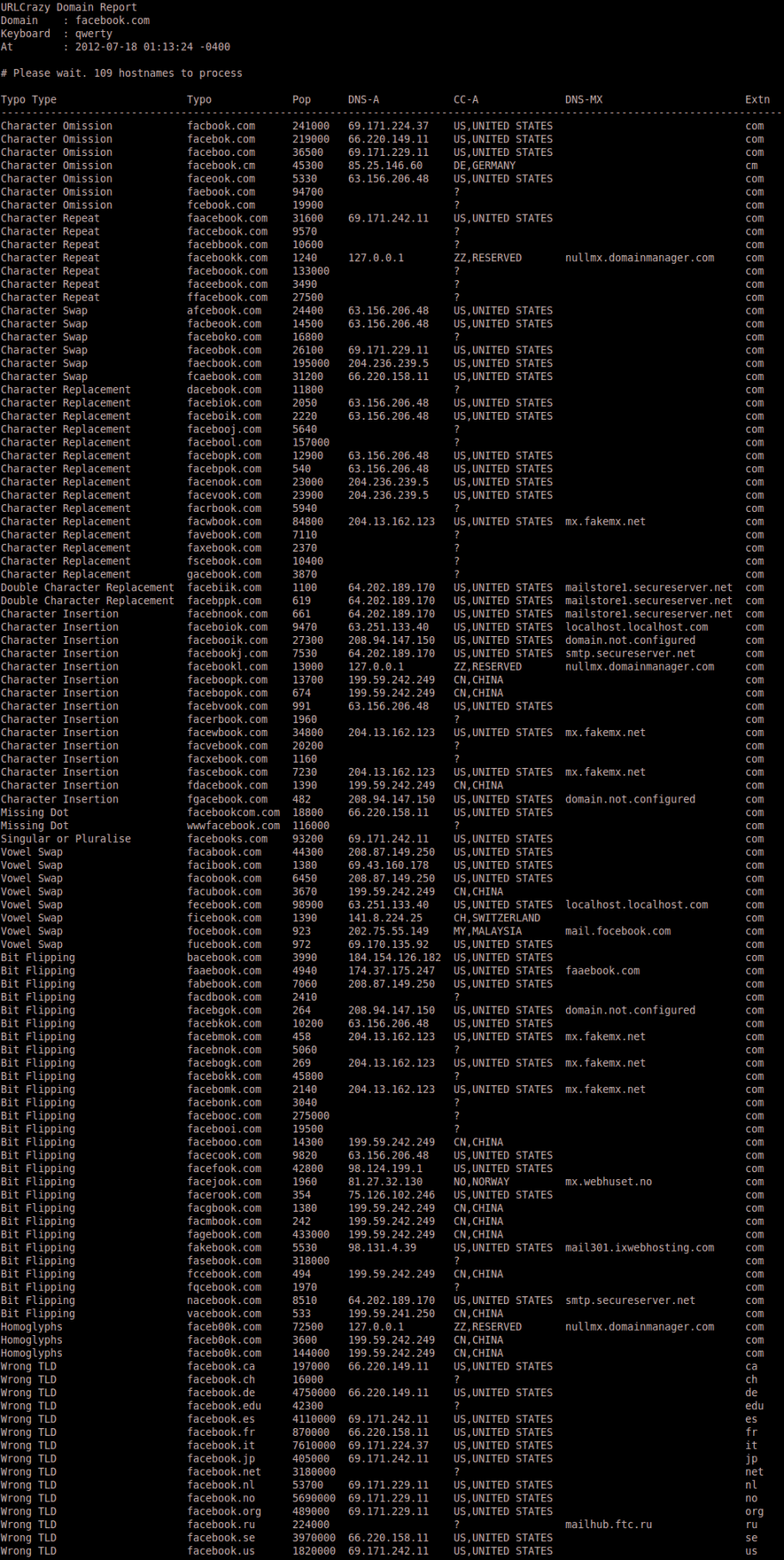
Sample Report

Types of Domain Variations Supported

Character Omission
These typos are created by leaving out a letter of the domain name, one letter at a time. For example, www.goole.com and www.gogle.com

Character Repeat
These typos are created by repeating a letter of the domain name. For example, www.ggoogle.com and www.gooogle.com

Adjacent Character Swap
These typos are created by swapping the order of adjacent letters in the domain name. For example, www.googel.com and www.ogogle.com

Adjacent Character Replacement
These typos are created by replacing each letter of the domain name with letters to the immediate left and right on the keyboard. For example, www.googke.com and www.goohle.com

Double Character Replacement
These typos are created by replacing identical, consecutive letters of the domain name with letters to the immediate left and right on the keyboard. For example, www.gppgle.com and www.giigle.com

Adjacent Character Insertion
These typos are created by inserting letters to the immediate left and right on the keyboard of each letter. For example, www.googhle.com and www.goopgle.com

Missing Dot
These typos are created by omitting a dot from the domainname. For example, wwwgoogle.com and www.googlecom

Strip Dashes
These typos are created by omitting a dash from the domainname. For example, www.domain-name.com becomes www.domainname.com

Singular or Pluralise
These typos are created by making a singular domain plural and vice versa. For example, www.google.com becomes www.googles.com and www.games.co.nz becomes www.game.co.nz

Common Misspellings
Over 8000 common misspellings from Wikipedia. For example, www.youtube.com becomes www.youtub.com and www.abseil.com becomes www.absail.com

Vowel Swapping
Swap vowels within the domain name except for the first letter. For example, www.google.com becomes www.gaagle.com.

Homophones
Over 450 sets of words that sound the same when spoken. For example, www.base.com becomes www.bass.com.

Homoglyphs
One or more characters that look similar to another character but are different are called homogylphs. An example is that the lower case l looks similar to the numeral one, e.g. l vs 1. For example, google.com becomes goog1e.com.

Wrong Top Level Domain
For example, www.trademe.co.nz becomes www.trademe.co.nz and www.google.com becomes www.google.org Uses the 19 most common top level domains.

Wrong Second Level Domain
Uses an alternate, valid second level domain for the top level domain. For example, www.trademe.co.nz becomes www.trademe.ac.nz and www.trademe.iwi.nz

Bit Flipping
Each letter in a domain name is an 8bit character. The character is substituted with the set of valid characters that can be made after a single bit flip. For example, facebook.com becomes bacebook.com, dacebook.com, faaebook.com,fabebook.com,facabook.com, etc.

Tips

The output will often be wider than the width of your terminal. If this bothers you, output your report to a file or increase the width of your terminal.

Keyboard layouts supported are

• QWERTY
• AZERTY
• QWERTZ
• DVORAK

Is the domain valid?

UrlCrazy has a database of valid top level and second level domains. This information has been compiled from Wikipedia and domain registrars. We know whether a domain is valid by checking if it matches toplevel and second level domains. For example, www.trademe.co.bz is a valid domain in Belize which allows any second level domain registrations but www.trademe.xo.nz isn’t because xo.nz isn’t an allowed second level domain in New Zealand.

Popularity Estimate

We can estimate the relative popularity of a typo by measuring how often that typo appears on webpages. Querying goole.com for the number of search results for a typo gives us a indication of how popular a typo is. The drawback of this approach is that you need to manually identify and omit legitimate domains such as googles.com For example, consider the following typos for google.com.

25424 gogle.com
24031 googel.com
22490 gooogle.com
19172 googles.com
19148 goole.com
18855 googl.com
17842 ggoogle.com

IP Address

An IP address for a typo domainname indicates it is in use. Tip: An IP repeating for multiple typos or IPs in a close range shows common ownership. For example, gogle.com, gogole.com and googel.com all resolve to 64.233.161.104 which is owned by Google.

Country Code Database

http://en.wikipedia.org/wiki/Top-level_domain

http://en.wikipedia.org/wiki/Country_code_top-level_domain

2nd level domains here: http://www.iana.org/domains/root/db/

See Also

http://en.wikipedia.org/wiki/Wikipedia:AutoWikiBrowser/Typos

http://en.wikipedia.org/wiki/Wikipedia:Typo

http://en.wikipedia.org/wiki/Typosquatting

Strider is tool with similar aims and is produced by Microsoft http://research.microsoft.com/csm/strider/

Appearances

Steven Wierckx wrote an article about URLCrazy at www.ihackforfun.eu.

Read Article

Credits

Authored by Andrew Horton (urbanadventurer). Andrew is a security consultant.
Thanks to Ruby on Rails for Inflector which allows plural and singular permutations.
Thanks to Wikipedia for the set of common misspellings, homophones, and homoglyphs.
Thanks to software77.net for their IP to country database